7 algoritmov, ktoré by mal vedieť každý programátor

Ako študent programovania ste sa počas svojej kariéry pravdepodobne naučili veľa rôznych algoritmov. Znalosť rôznych algoritmov je pre každého programátora úplne zásadná.

S toľkými algoritmami môže byť náročné sledovať, čo je podstatné. Ak sa chystáte na pohovor alebo si len zdokonalíte svoje schopnosti, tento zoznam to relatívne uľahčí. Pokračujte v čítaní, keď uvádzame zoznam najdôležitejších algoritmov pre programátorov.

1. Dijkstrov algoritmus

Edsger Dijkstra bol jedným z najvplyvnejších počítačových vedcov svojej doby a prispel k tomu mnoho rôznych oblastí výpočtovej vedy, vrátane operačných systémov, konštrukcie kompilátorov a podobne viac. Jedným z najpozoruhodnejších Dijkstrových prínosov je vynaliezavosť jeho algoritmu najkratšej cesty pre grafy, známeho tiež ako Dijkstraov najkratší cesta algoritmus.

Algoritmus Dijkstra nájde jedinú najkratšiu cestu v grafe zo zdroja do všetkých vrcholov grafu. Pri každej iterácii algoritmu sa pridá vrchol s minimálnou vzdialenosťou od zdroja a takým, ktorý v súčasnej najkratšej ceste neexistuje. Toto je chamtivá vlastnosť, ktorú používa Djikstraov algoritmus.

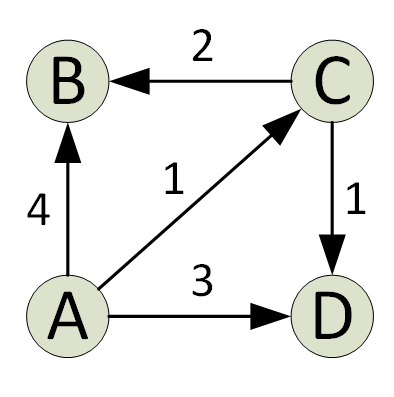
Algoritmus je obvykle implementovaný pomocou sady. Algoritmus Dijkstry je veľmi účinný, keď je implementovaný s min. najkratšiu cestu nájdete za iba O (V+ElogV) čas (V je počet vrcholov a E je počet hrán v danom grafe).

Algoritmus Dijkstry má svoje obmedzenia; funguje iba na smerovaných a neorientovaných grafoch s hranami kladnej hmotnosti. Pre negatívne hmotnosti je zvyčajne výhodnejší Bellman-Fordov algoritmus.

Pohovorové otázky bežne obsahujú Djikstrov algoritmus, preto dôrazne odporúčame porozumieť jeho zložitým podrobnostiam a aplikáciám.

2. Zlúčiť zoradiť

V tomto zozname máme niekoľko triediacich algoritmov a zlučovacie triedenie je jedným z najdôležitejších algoritmov. Je to účinný triediaci algoritmus založený na programovacej technike Divide and Conquer. V najhoršom prípade môže zlúčené triedenie zoradiť „n“ čísla iba za čas O (nlogn). V porovnaní s primitívnymi technikami triedenia ako napr Bublinkové triedenie (čo trvá 0 (n^2) času), triedenie zlúčením je vynikajúco efektívne.

Súvisiace: Úvod do zlučovacieho algoritmu triedenia

Pri zlučovacom triedení je pole, ktoré sa má triediť, opakovane rozdelené na podskupiny, kým každý podradník pozostáva z jedného čísla. Rekurzívny algoritmus potom opakovane zlučuje podskupiny a triedi pole.

3. Rýchle triedenie

Quicksort je ďalší algoritmus triedenia založený na programovacej technike Divide and Conquer. V tomto algoritme sa najskôr vyberie prvok ako pivot a celé pole sa potom rozdelí okolo tohto pivotu.

Ako ste pravdepodobne uhádli, dobrý pivot je rozhodujúci pre efektívne triedenie. Pivot môže byť buď náhodný prvok, mediálny prvok, prvý prvok alebo dokonca posledný prvok.

Implementácie rýchleho triedenia sa často líšia v spôsobe, akým si vyberajú pivot. V priemernom prípade quicksort zoradí veľké pole s dobrým pivotom len za čas O (nlogn).

Všeobecný pseudokód rýchleho triedenia opakovane rozdeľuje pole na pivot a umiestňuje ho do správnej polohy podoblasti. Vľavo tiež umiestni prvky menšie ako čap a napravo prvky väčšie ako čap.

4. Hĺbkové prvé vyhľadávanie

Hĺbkové prvé vyhľadávanie (DFS) je jedným z prvých grafických algoritmov, ktoré sa učia študenti. DFS je účinný algoritmus, ktorý sa používa na prechádzanie alebo vyhľadávanie v grafe. Môže byť tiež upravený tak, aby sa používal pri prechádzaní stromov.

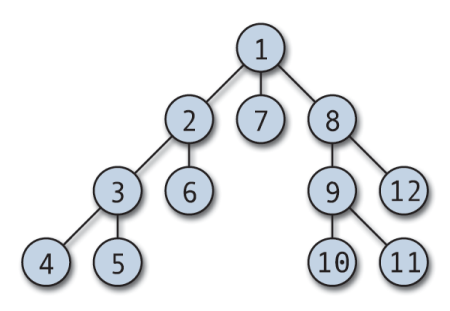
Prechod DFS môže začať z ľubovoľného ľubovoľného uzla a ponorí sa do každého susedného vrcholu. Algoritmus sa vracia, keď neexistuje žiadny nenavštívený vrchol alebo je slepá ulička. DFS sa zvyčajne implementuje so zásobníkom a booleovským poľom na sledovanie navštívených uzlov. DFS je ľahko implementovateľný a mimoriadne efektívny; funguje (V+E), kde V je počet vrcholov a E je počet hrán.

Medzi typické aplikácie prechodu DFS patrí topologické triedenie, detekcia cyklov v grafe, hľadanie cesty a hľadanie silne prepojených komponentov.

5. Hľadanie do šírky

Breadth-First Search (BFS) je tiež známe ako prechod objednávok stromov na úrovni úrovne. BFS funguje v O (V+E) podobne ako algoritmus DFS. BFS však namiesto frontu používa front. DFS sa ponorí do grafu, zatiaľ čo BFS prechádza grafom po šírke.

Algoritmus BFS využíva front na sledovanie vrcholov. Nenavštívené susedné vrcholy sú navštívené, označené a zaradené do poradia. Ak vrchol nemá žiadne susediace vrcholy, vrchol sa z frontu odstráni a preskúma.

BFS sa bežne používa v sieťach typu peer-to-peer, najkratšia cesta neváženého grafu a na nájdenie stromu minimálneho preklenutia.

6. Binárne vyhľadávanie

Binárne vyhľadávanie je jednoduchý algoritmus na nájdenie požadovaného prvku v triedenom poli. Funguje to tak, že pole opakovane rozdelíte na polovicu. Ak je požadovaný prvok menší ako stredný prvok, ľavá strana stredného prvku sa spracuje ďalej; v opačnom prípade sa pravá strana zníži na polovicu a znova sa prehľadá. Proces sa opakuje, kým sa nenájde požadovaný prvok.

Časová náročnosť binárneho vyhľadávania je O (logn), čo ho robí veľmi efektívnym pri hľadaní lineárnych polí.

7. Minimálne algoritmy pre preklenovací strom

Minimálny spanning tree (MST) grafu má minimálne náklady spomedzi všetkých možných spanning stromov. Náklady na klenutý strom závisia od hmotnosti jeho okrajov. Je dôležité si uvedomiť, že môže existovať viac ako jeden minimálny klenutý strom. Existujú dva hlavné algoritmy MST, a to Kruskalov a Primov.

Kruskalov algoritmus vytvára MST pridaním hrany s minimálnymi nákladmi do rastúcej sady. Algoritmus najskôr zoradí hrany podľa hmotnosti a potom pridá hrany k MST od minima.

Je dôležité poznamenať, že algoritmus nepridáva hrany, ktoré tvoria cyklus. Kruskalov algoritmus je preferovaný pre riedke grafy.

Primov algoritmus tiež používa chamtivú vlastnosť a je ideálny pre husté grafy. Ústrednou myšlienkou Primovho MST je mať dve odlišné sady vrcholov; jedna sada obsahuje rastúci MST, zatiaľ čo druhá obsahuje nepoužité vrcholy. Pri každej iterácii je vybraná hrana minimálnej hmotnosti, ktorá bude spájať tieto dve sady.

Algoritmy minimálneho spanning stromu sú nevyhnutné pre klastrovú analýzu, taxonómiu a vysielacie siete.

Efektívny programátor ovláda algoritmy

Programátori sa neustále učia a rozvíjajú svoje schopnosti a existuje niekoľko základných zásad, v ktorých musí každý ovládať. Skúsený programátor pozná rôzne algoritmy, výhody a nevýhody každého z nich a ktorý algoritmus by bol pre daný scenár najvhodnejší.

Úvod do algoritmu triedenia Shell

Aj keď škrupinové triedenie nie je najefektívnejšia metóda, začiatočníci môžu jeho cvičením veľa získať.

Čítajte ďalej

O autorovi